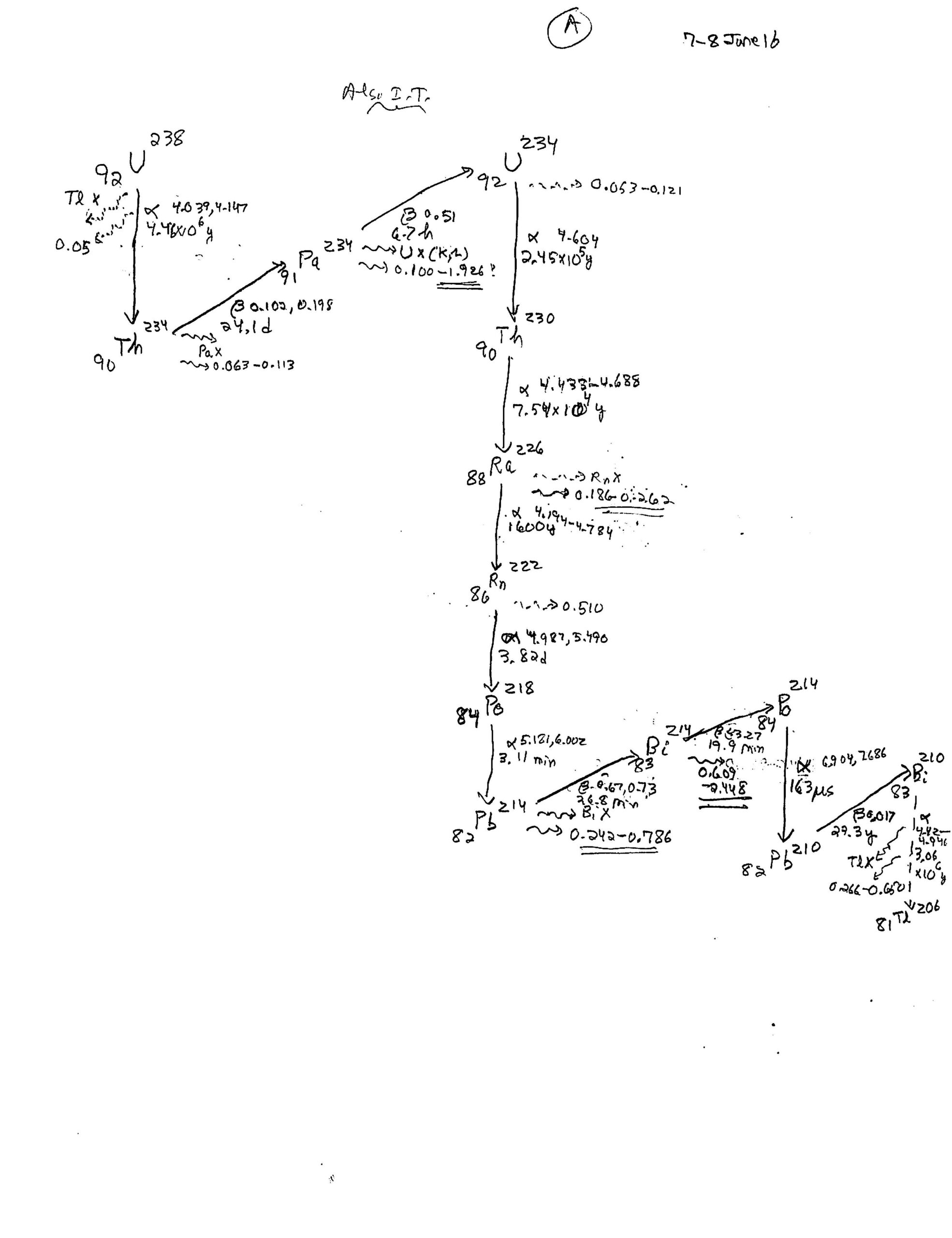
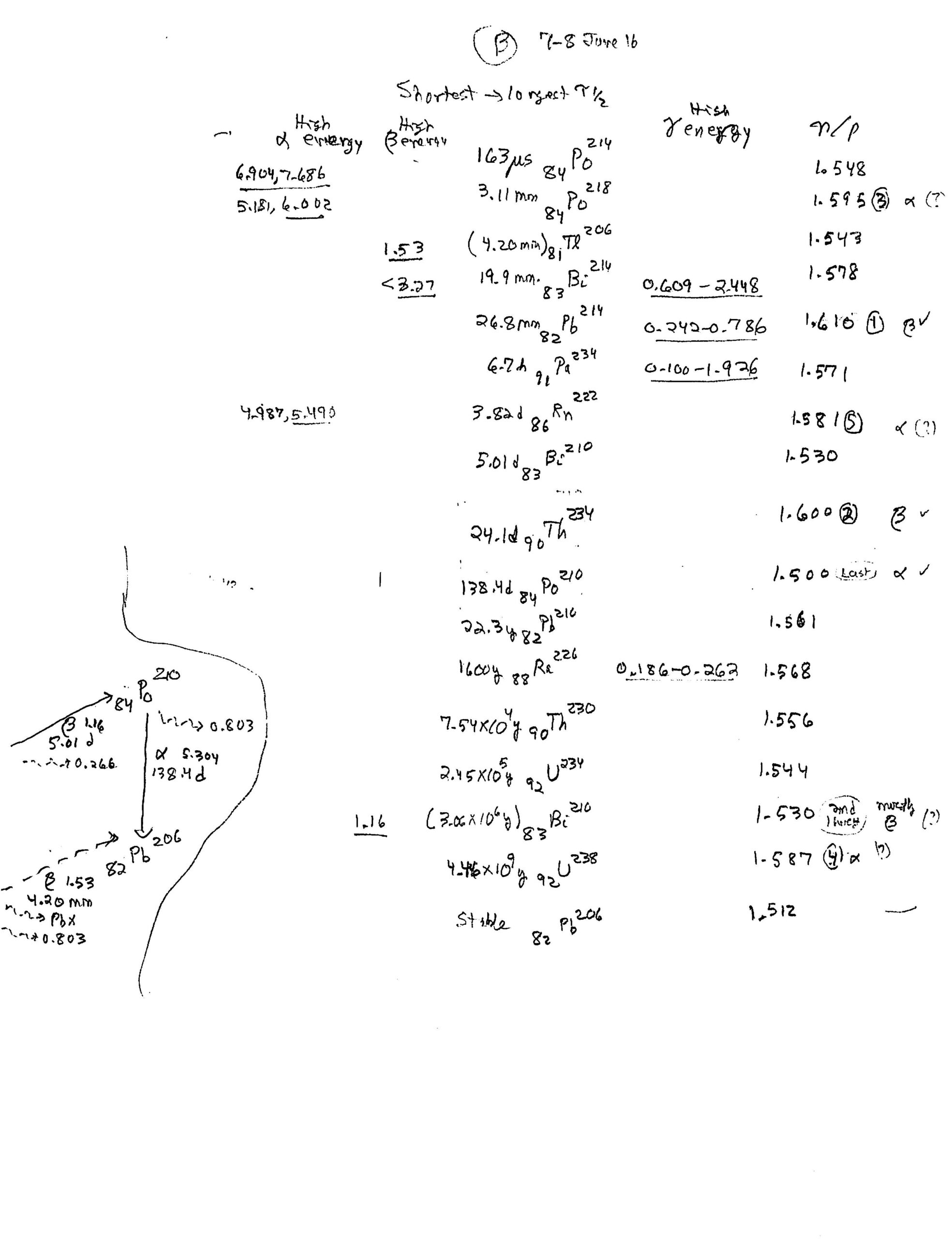
Sort of a one-stop-shop for model rocketry theory, experiments, and data analysis for a high-school class, or an advanced middle-school class such as we have at the Las Cruces Academy:
Tsiolkovsky derived the equation for the final speed of a rocket in free space (no air drag) in 1903! I have a derivation here, plus an elaboration that goes on to consider air drag and gravity for a surface launch, and another one that looks at how a rocket has to be designed with propellant, payload, and basic infrastructure (the shell, we may say).
Our students at the Las Cruces Academy did rocket launches in the desert, measuring the altitude achieved with geometric measurements.
Some pictures are useful. Check out the link on the LCA News and Events page.
The results for altitude vs. rocket motor impulse are summarized in a spreadsheet. Altitude looks to be linear in impulse, in line with numerical simulations I performed. We had to be very careful with our measurements, btw, since small errors lead to big errors in altitude.
A sideline: where does the kinetic energy go, partitioned between exhaust gases and the rocket? At burnout for a serious rocket, there’s more in the gases than in the payload that’s left.