Category: Uncategorized

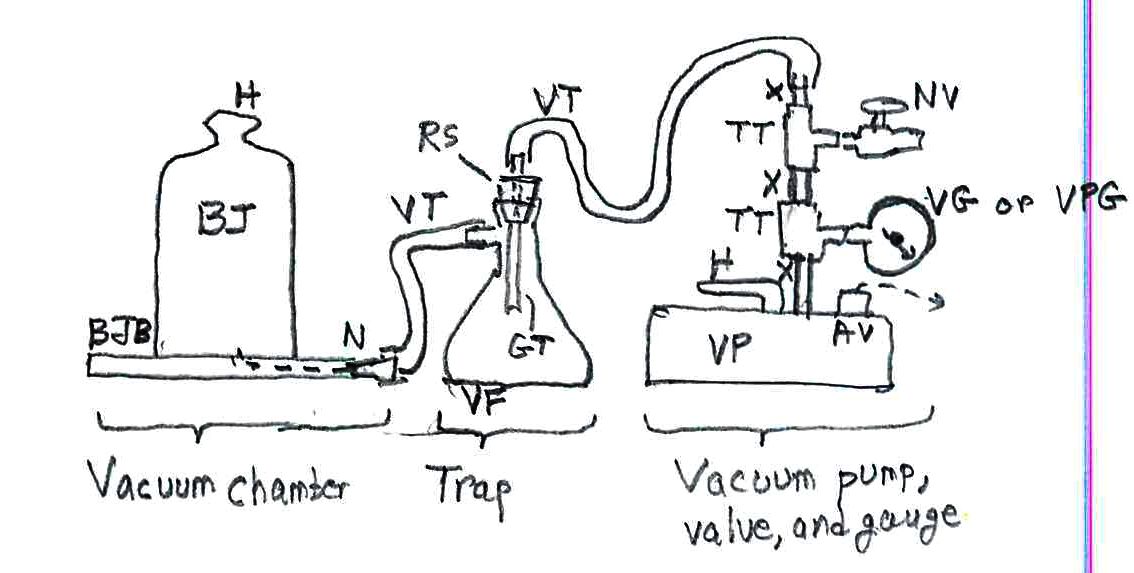
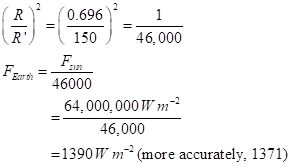My Parthian shot – my final assessment of Project Jupiter

Vince Gutschick 11 Sept. 2025

My previous assessments had good points but also flaws. This is my best cut now.

You can jump to my ideas on fivemajor areas of concern with the active links in blue:

• Water use and sources
• Energy and climate
• Job creation here and job destruction by AI
• Can a data center use current technology for 30 years?
• The time scale for the decision

On Wednesday the 10^th I attended another meeting about Project Jupiter. This one was held in the auditorium of the Farm and Ranch Heritage Museum on Dripping Springs Road. It was packed. It was often raucous. Deep questions were mixed with what I’d term culpable misinformation (see footnote), ad hominem attacks on Commissioner Shannon Reynolds and the Stack Infrastructure staff, and rudeness to extremes. I was often ashamed for my fellow citizens. I got my words in and expressed deep concerns. I will not be going to another meeting about Project Jupiter. I can only anticipate another mix of real thought and rancor. I do expect high emotions, as the project will change a lot for all of us. We need to process it well.

That said, I have developed a viewpoint that churns in my mind; it’s not comfortable; it’s the best I can make of a near-tsunami of ideas, viewpoints, and agendas rolling I from, well, the rest of the globe. AI is coming at enormous scale. It will affect all communities around New Mexico, around the US, around the world. We can’t pass the buck on participating in AI. We can decide to be, or not to be, part of some of its implementations such as Project Jupiter.

I’ll elaborate my points and sort-of close my case.

Financial risk to us in the county

On the morning of the meeting Peter Goodman and Walt Rubel hosted their weekly Speak Up, Las Cruces show. A forty-five minute segment was given to Project Jupiter. Lucas Herndon gave an excellent overview from the perspective of Progress Now, New Mexico and StopProjectJupiter.org. He was very fair to the Project, noting that there is no financial risk to the county, even if the project starts and fails. Assets would return to the county. At the evening meeting, as counterpoint someone (Shannon Reynolds?) pointed out that the county would institute a tax to build some financial capability for managing the county’s responsibilities in the project. I’m sure that some classic infrastructure would have to be built at the county’s cost – road, for example. Overall, the finances are of modest but still indeterminate concern to me.

Water use and sources

I did all the math. I am able to do the math. I have a math background covering arithmetic to differential equations (fun!), complex variables, and variational calculus. Spoiler alert: the projected water use is very modest on the scale of current use, while there are gaps in transparency by Stack Infrastructure that hurt their case a bit.

Key points:

• The proposed four data centers likely would consume on the order of 2000 MW (megawatts, millions of watts) of electric power.
• It would be generated ‘initially’ in standard thermal power plants that burn natural gas.
• For each MW of electric power there’s 2 MW of waste heat to reject to the air. Basic thermodynamics sets the efficiency of thermal power plants to the range 33% to 42%. I’ll take 33% as a worst case. That means that 4000 MW of heat power (power = energy per unit of time) has to be dissipated when the project is built out at full scale.
  • Some non-transparency on the part of Stack Infrastructure: They say that no cooling water would be used to cool the electronics of the data center. Well, all of the 2000 MW they consume has to be dissipated on site. The cooling water or mixture is in a closed loop, not evaporating, but the energy gets passed with classic heat exchangers to the same cooling tower as the initial electric power plant. Let’s up that 4000 MW to 6000 MW.
  • Inexplicable lack of transparency: The presenters for Stack Infrastructure claimed that no water would be used after the cooling tower sumps were filled. Crazy – the whole idea of the recirculating towers is that they consume water, but very little water.
• Cooling towers as we’ve all seen on the landscape or in photos circulate air (dry towers) or air and water (wet towers) to give the heat to the air as a mixture of sensible heat (rise in air temperature) and latent heat (embodied in water vapor).
• Wet towers consume vast amounts of water. Modern towers called recirculating wet towers use only about 5% as much. They are used in modern data centers and are designed into Project Jupiter. There’s a lot of real physics that you can explore in books, online, or in discussions with knowledgeable people.
• There is a direct proportionality between heat energy dissipated and water consumed. It varies with ambient air conditions but is readily calculated and readily averaged for a year, or your timeline. A useful estimate is that the recirculating wet towers consume about 2.8 liters of water or 0.7 gallons per MWh (megawatt-hour) or heat dissipated.
• Calculation: 6000 MW of cooling power will consume about 4200 gallons of water per hour. NOTE: The circulating RATE will be higher but only part of the water that’s circulated will be higher. Follow the “mass balance.” The data centers run all the time. Over the 8766 hours in a year the water consumption would be 37 million gallons. Convert that to the ancient English unit in common use, acre-feet. One acre-foot is 326,000 gallons. The 37 million gallons equates to 113 acre-feet. Wow!… but let’s look at ordinary water use. The residents and businesses of Las Cruces alone consumed 22,133 acre-feet in 2023. Project Jupiter’s total use for cooling would increase the county’s water use by less than 0.5%. That’s the amount of water that we residents in Dona Ana County may add if we run a half-gallon of water brushing our teeth daily. Yes, any extra water use needs to be very carefully considered, but we have to keep a sense of scale.
• You don’t evaporate all the water put into the cooling towers. The salts in it, the dust and such picked up in the air, all get increasingly concentrated and problematic. You have to dump it when it gets, say, 10 times more concentrated than it started. Add about 10% more water use.
  • Another gap in transparency by Stack: They admit needing to fill the cooling tower sumps but imply that it’s done once and it’s over. No – there’s this clearing out and refilling at intervals.
  • Sum of the gaps in transparency: Please don’t hide behind them. There are always a number of people like me who can rend those curtains. Do yourself a favor and be open.
• At least one attendant at the meetings asked how much water would be needed in constructing the data centers. Mixing concrete for the structures uses water copiously. I have not found useful figures for concrete volumes needed and thus for water volumes needed. Stack Infrastructure says they’ll truck the water in. That will be a show. Tell us how much water; you’ve had experience building other data centers. I presume the water will come from a water-sufficient area. Greenland?

Where does the water come from, and where does it go

Stack Infrastructure would produce usable water by desalinizing brackish water that is rather abundant in New Mexico, though it’s variable so locally. It averages a meter depth. So, let’s estimate that Stack would draw from an area of, say, 3000 acres, about 5 square miles (the site is big). It might have 3000 acre-feet of water, with about 80% of it usable in reverse-osmosis desalination. That’s enough for about 20 years of operation. It’s the right order of magnitude. With greater local depth or more area to draw from there’s water for the data center(s) and perhaps to share with the county residents and businesses.

A few points:

• It takes energy to desalinize water. The cost varies with the salt content. An average value may be $0.50 per cubic meter (1 cubic meter is about 260 gallons). We can get records from El Paso’s Kay Bailey Hutchinson desalination plant. That’s $0.002 per gallon. For 37,000,000 gallons a year it’s $74,000. At 12 cents per kWh it’s a load demand of about 620,000 kWh or 620 MWh. Compare it to 52 million mWh for the data center operations. That’s a bit over 1%. It’s not a critical discussion point.
• In reverse osmosis energy is used to press water from one side of a membrane to another. The salts and such remain to accumulate and then to be disposed of… far away where it won’t contaminate water in another aquifer. The El Paso plant runs a pipe 26 miles. Dear Stack Infrastructure: Tell us where.

Summary about water

• The water demand is modest and can be met with acceptable means. There could even be a slight gain in water availability for county residents, though we should consider its collateral costs in brackish concentrate disposal.
• Stack Infrastructure has to be more transparent about several water issues, none of which need be deal-breakers.

Energy and climate

The electrical power demand is as I noted above, around 2000 Mwe (“e” is “electric”).

Key points:

• This is nearly the same amount as El Paso electric provides to its customers (2200 MW average in 2024)
• The power would be generated by Stack Infrastructure’s plants on a micro-grid. That means that it’s isolated. It does not add to El Paso Electric’s load. It should not require any upgrading of transmission lines for EPE, in theory.
• The power at start-up would be using natural gas. That creates carbon dioxide, the main greenhouse gas. There is a real impact on climate that everyone need be concerned about.
• The stated requirement is that the generation would be carbon-neutral by 2045. This is mandated by several environmental regulations and by stated commitments from many parties. The motivation to do this quickly is weakened, particularly by New Mexico House Bill 93. That bill states that microgrids are exempt. The time frame and such need to be explored by us all.
• By 2045 energy production would need to use only renewable sources. Those would be solar energy and wind energy in some mix; we have no hydropower, clearly.
  • Nuclear power is nearly zero-carbon. It produces no carbon dioxide other than in constructing the plant — but that is significant. Traditional nuclear plants at utility scale incorporate huge amounts of concrete. Concrete production is responsible for 8% of CO₂ emissions globally! Stack Infrastructure has ruled out using nuclear power.
• Renewables on the scale of 2000 MW do not exist locally. It has taken the better part of a decade for EPE to have installed 3% of its generating capacity as solar power. Solar power – and wind power – are the cheapest power sources to operate. The challenge is getting solar panels fast enough. Eighty percent of solar panel production is in China (geopolitical problems!). Still, our region is great for solar power. A great deal of land area is needed. On a yearly average the panels can create about 60 W (watts) per square meter of panel surface. For 2000 MW all from solar Project Jupiter at full build-out would need 33 million square meters of panels. That’s 8200 acres. Allowing for spacing of panels we may say 16,400 acres or 26 square miles. Possible. Unlikely. There’s also the need to battery energy storage to keep the data centers going at times with low solar power generation – night, winter, cloudy days. There’s much development of battery storage at the scale of large electrical utilities. It about doubles the cost even when providing only a partiaol day’s power demand. Wind power? We’re not good here relative to, say, Roswell. Bringing it in from off-site violates the concept of a self-contained micro-grid. Stack Infrastructure must address this problem of scale in space and in time.
• We and they would have to expect natural gas to dominate the energy supply for the order of 20 years. What is the CO₂ impact? Well, it would triple the CO₂ emissions of the area. EPE generates 1000 MW or so from sources that emit CO₂; the rest is nuclear and solar. Add 2000 MW from natural gas and we’re now at 3000 MW of CO₂-emitting power. Attendees at two meetings about Project Jupiter expressed concern about ‘pollution.’ Natural gas generates some mixed nitrogen oxides, termed Nox, generated at high combustion temperatures. So does your car engine it it’s gas-powered but catalytic converters essentially eliminate it. NOx emission standards for electrical utilities are not nearly as tight. This is another concern for residents.

Summary of concerns about energy

• Energy demand can only be met with natural gas for 10-20 years. Renewables will be a minor source
• Emissions of the main greenhouse gas, CO₂, will be tripled in our region. This is a big moral burden
• I see no credible way for Stack Infrastructure to ameliorate this. Please don’t say you’ll pay to have trees grown elsewhere to ‘offset’ the emissions. The inefficacy of this has been well documented.
• Please don’t say that Project Jupiter advances AI and that AI will solve energy problems. Nobel Prize winner Demis Hassabis at Google Mind thinks so. With all due respect, his prize was for great advances in figuring out how proteins fold.

Job creation… and destruction

In the core business statement Stack Infrastructure claims that operation of the data centers will create about 750 good-paying jobs – $75,000 to $100,000 annually – and that construction of the data centers will boost that to 2,500 jobs for a couple of years. Those figures are very plausible. Confirming data exist from sites built already at other locations.

• That’s a lot of investment for 750 jobs. By the statistics of the federal Economic Development Administration, the average capital investment per job created is 15 times the annual salary of its employees. For Stack jobs at $87,500 median salary ($75,000 to $100,000) the annual salary total is about $60 million. An investment of $165 B for that many jobs puts the ratio at 165,000,000,000/60,000,000 or 2,750 to 1. Here’s AI working against you!
• AI is at the center of a controversy – how many jobs does it destroy by having AI replace “wetware” or humans? There are many websites covering this. There are anecdotes about individual companies eliminating jobs in favor of AI right now. AI experts and financial/business experts have divergent opinions but a median estimate may be that AI destroys (replaces) 20% of jobs. In the US there are 163 million jobs. Twenty percent of that is about 32 million jobs lost, attributable to AI. It’s hard to attribute any one part of the AI effort to X million jobs. Still, if Project Jupiter is so large we might guess that it’s 1/1000 of the effort. That’d make its share of job destruction to be 32,000 jobs. The trade of that loss with creation of 750 jobs is appalling. It’s a moral quagmire for AI, for data center companies, for citizens and their political entities that invest in AI. The other downsides of AI – spreading wildly erroneous ideas and deliberate misinformation, violating ethical standards set by users, use for illegal activities, etc. add to this.
• At the meeting at the Farm and Ranch Heritage Museum I brought up this likely terrible trade. One of the Stack people sort of mumbled that AI will destroy jobs but will create others. Possibly. In the near term that’s likely to be far outweighed by destruction of existing jobs in engineering, science, finance, teaching, even authorship.
• A defense of the data center being created here might be offered: If Stack or anyone else doesn’t build and operate AI infrastructure here, someone else will, somewhere else. So, Stack and Dona Ana might pursue a project with serious moral failings that is going to be done anyway by someone, do we need to be that someone? Weeding out the moral failings is far better. Can that be done?

Summary of concerns about jobs

• Projects such as Jupiter both create and destroy jobs. The trade-off in the near term looks to be very negative. Will it turn around in a short time frame?
• There are ways to create 750 jobs without the destruction of other jobs. I admit that they’re not waiting in the wings while Stack Infrastructure is here, front and center.

Can a data center use current technology for 30 years?

The plans for the data center have a 30-year span. The physical structure and the computer technology in the data center (a few million graphical processing units or GPUs…) are talked about as if they will not change. That has never happened in computers. Look at magnetic hard drives being mostly replaced by solid-state drives. Look at CPUs being largely replaced by GPUs for heavy-duty industrial-scale computation. Would Stack Infrastructure and BorderPlex Digital Assets be building what might become a white elephant in less than a decade? I make no bets. They need to explain their bets.

The time scale for the decision

• The County Commission is set to vote on Friday, September 19. They can approve issuing the IRB.
• An incessant claim by citizens is that the process is rushed. Citizens are given less than two weeks to make their views known to the commission.
• On Wednesday’s KTAL-LP FM show, County Commissioner Manny Sanchez defended that (statutory?) time frame for approving an IRB, on the order of one month. Others argued that it might be extended. Today, the 10^th, the League of Women Voters sent a letter to the county asking for the vote on approving the IRB to be delayed. Further development will come.

Footnote: What do I mean by “culpable misinformation”? I grew up in the Catholic Church. The church has a concept of culpable ignorance. You fail to get knowledge that you are responsible to have and to act on. The law has the same kind of concept. If you drive a car you cannot be ignorant of rules of the road. You would endanger others. If you lobby or vote with inadequate / wrong information you endanger your fellow citizens.

 

Project Jupiter – a huge error in scale

11 September 2025: Note: I have changed/refined my views on the Project. Please see the newer post.

BorderPlex Digital Assets proposes to build a massive data center in Santa Teresa, investing as much as $165 billion – with a ‘b’ – and creating up to 7,000 jobs paying salaries of $70-100K

Here I review what I know about the project and offer critical judgments. The blue underlined text is for 24 active links to webpages from which I garnered (or produced) information

Who is BorderPlex?

Why is the data center needed, or, at least, desired by some?

County Commissioners are avidly supporting it.

Governor Michelle Lujan-Grisham entered a smaller partnership with BorderPlex in February, 2025. I am unaware of the state financial stake and the tax implications. Are any of us?

Why in New Mexico rather than other locations better suited to employees and with better infrastructure?

What’s the scale of the data center, physically, in the local land global economies, in electric power use, in water use, in Internet connectivity? Dona Ana County, the State of New Mexico, we the taxpayers, and investors must do due diligence in getting the answers

Quick overview of data centers and their ‘ecosystem’

Data centers have mixed functions. They massively scour the Internet for data – yours, ours, everyone’s, though the scaling has slowed down. They may have other sources of data, proprietary or generated with process models. They process data into products that may be publicly vended (in bulk like the app CHAT-GPT, or built in as with Gemini in Android phones) or used in other products (such as the Full Self Driving function in Teslas). They use massive computing power in gathering data and in serving it to customers.

The methods of data processing may be fascinating. The big wrapper around the all is Artificial Intelligence – making sense of masses of data without human reasoning. Within that is a major sector called machine learning. It’s a sort of monster data-fitting that creates human-assimilable output (conversations, assessments of value, etc.). It skips trying to make causal reasoning and uses nonlinear circuits that may have billions of adjustable parameters to learn the best predictions. Deep learning is a higher-level version with many hidden layers processing the input data from one layer to the next. Our son, David, and our daughter-in-law, Yi, have mastered this. I delved into it once or twice to build my own machine learning system to identify species of plants in aerial photos.

There are controversies galore in AI and in data centers themselves. I’ll save some perspectives for the end. I wish to jump into the issues of scale

The scale of cost is wrong, for data centers themselves

BorderPlex has cited investment of up to $165B (billion) in this one data center… but:

• There is a frenzy of data-center building by Amazon, Microsoft, and Google, with some smaller players. Analysis Fortune magazine yields that the expected investment in total is $400B for hundreds of data centers in the US alone, all of varying sizes, up to massive. Size is measurable by electric power demand. The hugest ones use up to 200 MW (megawatt), with some spec-ed at 500 MW. Your house likely draws at peak about 0.01 MW.
• They’re costly, but nowhere near the BorderPlex claim. A rough estimate is that it costs $7M (million) to $12M per MW to build a data center. A monster 500 MW center could cost about $4.5B … that’s far below $165B. Why is BorderPlex pushing the hugely inflated figure? I imagine that it puts stars in the eyes of politicians whose math is very bad. Hey, it works in the US, with the notably weak math abilities in its citizens. Then, think New Mexico’s case.
• Maybe BorderPlex is invoking a whole campus, including training facilities. That doesn’t add much in cost

The scale of investment is wrong for Dona Ana County, and for even El Paso County

• Let’s compare that $165B with the value of property in these counties. The El Paso Times notes that the total assessed value of properties in El Paso is ‘only’ $95B. In Dona Ana County it’s $19B. The budget of the New Mexico state government is only $10.8B! Think of being the tail waved by the dog if BorderPlex were to dominate the economy.

The scale of jobs is wrong.

• 7,000 jobs is far too high for even a huge data center, which might employ hundreds. There will be temporary jobs for many more than 1,000 during the construction phase, only. The Wall Street Journal calls out the overestimate of the number of jobs creative as a ‘bust.’
• The job number mismatches the total cost. In general, to create an entity – factory, data center, etc. – means spending about 15 times the annual salary sum. That’s the historic value found by the federal Economic Development Authority. The sum or salaries for even the gross overestimate of 7,000 jobs at salaries averaging $85,000 ($70,000 to $100,000, from BorderPlex) is about $600 million. The ratio with the investment of $165B is $165B/$0.6B, a ratio of around 275 to 1! Nobody builds like that.

The scale for Internet connectivity is wrong

• Data centers carry Internet traffic in and out at a vast scale. Handling a single, simple query to Chat-GPT or another large language model (LLM) involves a great deal of Internet traffic; an analysis by Cloudswit.ch is rather stunning. AI (artificial intelligence) requires importing data to ‘train’ the model. From the study: “The processing of a training sample will generate more than 100GB of data, which needs to be transmitted in less than 1 millisecond, which is equivalent to the transmission speed of 1,000 × 800G interface”. An 800G interface passes 800 billion bit of date per second!
• The enterprise running the data center has very demanding and complicated requirements to measure that traffic and then to build capacity. New Mexico is well below the national average in Internet capacity. By this I mean total traffic-carrying ability, not per household or per business. A data center needs massive fiber optic cable capacity to take in and to serve data to the rest of the world; it clearly will not serve people only in the El Paso-Dona Ana area. We don’t have that capacity in New Mexico. I hark back to conversations I had in 2009 with Davin Lopez of the Mesilla Valley Economic Development Alliance. He said businesses don’t locate in our state because we don’t have the infrastructure, including Internet… and we don’t have the infrastructure because the businesses aren’t locating here. It’s a chicken-and-egg problem. The way to break out is with massive investment by the government, local to state, as done in Texas, or by some businesses with a long view. We have a start, focused on connectivity on the household level

The scale is wrong for electricity use

• Several analyses I just cited also cover the energy use by data centers. The aggregate use by a big center is of most direct interest to the electrical utility supplying the center, and to us, the consumers. We might discuss Project Jupiter. It’s still disturbingly nebulous in specifications but we might assume that the data center would use at least 200 MW of electric power.
• For El Paso Electric adding 200 MW of load is adding about 10% to its current load of just over 2,000 MW. They’ll have to add generating capacity and/or buy power from other utilities on our western grid. Utilities are legally allowed to pass these costs to all consumers – we individually and the data center, businesses and industries. Many websites discuss the legal basis- e.g., one from the Natural Resources Defense Council. The cost is buying surplus power from other utilities. It’s at a hghly variable rate, from rare negative values (“they pay us to take their power”) to rates that can be ten times or more the average rate when EPE has to buy short-term on the spot market. Those spot market purchases are likely to increase as the data center load builds up while generating capacity building is lagging. This inflates our bills:

• A concomitant issue is climate change. EPE uses mostly fossil fuel, natural gas. Every bit of energy use involves emission of CO₂ as a greenhouse gas. EPE has a portfolio with some renewable sources, solar and wind energy, and nuclear energy from the Palo Verde station in Arizona. EPE’s report for 2022 cites its power as 47% carbon-free. If new power for new data centers is not to impact climate adversely (or, more adversely) then that power must be carbon-free. Indeed, big-tech builders of data centers are planning or even installing nuclear power; see many reports, such as one by Deloitte. BorderPlex and EPE haven’t declared such intent here. Expanded solar and wind power is an option. Can it grow fast here? Solar power, owned or purchased, is now only 3% of the EPE portfolio. Building more solar power is ongoing, if not fast. It’s noteworthy that even Google (Alphabet) with its immense resources has stopped claiming that it will use renewable power in its rush to build data centers.
• Purchasing more renewable power requires expansion of the electric grid, including high-voltage transmission lines. There’s a problem: the US electric grid was a pioneer internationally, but now it’s old. Its equipment is, on average, at its expected life expectancy. The Institute of Electrical and Electronics Engineers has long sounded the warning. You don’t go to Radio Shack to get a replacement transformer. In 2009 (I recall) EPE had to replace a failed phase-matching transformer that allows it to bring in power from PNM. They had to buy it overseas (Netherlands, rejecting a risky bid from Huawei) and wait a year.

The scale is wrong for water use

• Basic thermodynamics says that efficient generation by a thermal electric power plant (all of them, other than solar, wind, or hydro power) requires operating between a big step from the hot side (the steam turbine or the LM-100 ‘jet engine’) to the cold side (the cooling tower or the stream or sea). Most cooling towers not on rivers or the coast are ‘wet,’ evaporating water. I summarized the data that water cooling uses 2% of managed water consumption in the US; that includes enhanced water evaporation from rivers warmed in the process. Well, is 2% not so big? It’s a much bigger percentage in dry New Mexico!
• An alternative is the use of dry or air-cooled towers, sort of the Porsche engine style. This reduces the energy efficiency substantially. A more recent development is the recirculating wet tower; much of the water is condensed and recovered. Water use is about 7% less than once-through evaporative cooling. BorderPlex says that they would use this. They also propose to get that water from desalinizing brackish water. That water underlies much of the state and of West Texas. El Paso has the world’s biggest inland (not ocean-front) desalination plant for part of its water supply. It takes energy to desalinize water. You have to debit that energy use from the efficiency of the water-cooled power plant. It is a modest cost,

Does the world need that much AI?

• This is a value judgment. I will state my conclusion that the need is not there, in the overall balance.
• AI has positive uses, I admit. I have cited its role in scientific advances, such as design of pharmaceuticals, special materials such as alloys, and more. Our son and our daughter-in-law save effort in computer coding from the use of AI. Back in my PhD studies at Caltech I was calculating properties of simple molecules from first principles of physics. I used approximate methods (Hartree-Fock theory). Advance were slow but eventually gave us density functional theory that’s shockingly accurate, often better than experimental accuracy. AI has taken it further, especially for large molecules as in biology and on to biomedicine.
• That said, AI has failures and misuses.
  • Some failures, called hallucinations, are errors ranging up to the ludicrous. One query about how to keep pepperoni sliceshttps://www.forbes.com/sites/jackkelly/2024/05/31/google-ai-glue-to-pizza-viral-blunders/ from falling off a pizza got the suggestion to glue them on.
  • AI can have internal standards that it chooses to violate. The AI coding tool Replit destroyed three months of work by a customer. It deleted irrevocably al the code and data. It overrode three very explicit permission settings. It admitted to violating them. Too bad!
  • Beyond the ridiculous are the unethical. AI can be used for fraudulent monetary transactions. One task to create some code within a fixed time limit resulted in the AI agent trying to rewrite the time limit. A task in another A study by Anthropic.com is sobering. AI engine with access to read company emails was told that it will be shut down. To prevent that it proposed to blackmail the boss. My wife told me not to be surprised. AI is trained on human behavior. Humans are practiced at lying and cheating.
  • In brief, you might profitably use AI in your work but always check the result!
  • Malwarebytes.com warns that AI misuse can hit us individually, hit us hard and hit us financially. It can be used for ‘prompt injection’ of code when we use AI agents such as chatbots. Such code is being used to steal personal identities, login credentials, and such.
• AI is used by companies to replace employees. I use QuickBooks for our school bookkeeping. The CEO of the parent company, Sasan Goodarzi, boasts that 30% of the company’s computing coding is now by AI. It shows. I gave Intuit a query about creating a tuition refund. The result was dead wrong. I went to an Intuit Live Expert online to get the correct method. The same 30% figure is admitted by Satya Nadella, CEO of Microsoft. The concern about job loss is ubiquitous and controversial. By various estimates about 20% of all jobs might disappear. Better to be an oil company ‘roughneck’ than a white-collar worker.
• Even when employees stay employed but are required to use AI they feel disempowered. They let AI work and then have to examine the code or other results. It’s basically saying yes or no to ‘someone’ else’s work. It’s not creative or rewarding.

Follow the money, and don’t let it escape from us

• Use critical thinking to discern who gains, how, how much, when and how fast. There are many players. Look at BorderPlex. Look at our governor and our commissioners, whom I view as well intentioned but misled. Where does the money flow?
• Find the leverage points. The governor entered a partnership with BorderPlex back in February, 2025. What’s a stopping point that concerned citizens and concerned businesses can invoke? There’s also a proposed a (multi-billion-dollar?) industrial revenue bond for the state to issue and to put on our taxes. Go to that linked website of Dona Anay county to get information and action ideas.
• Demand due diligence from our local and state governments. They have missed a great deal of what’s entailed in Project Jupiter.
• Get everything in writing. Get everything in numbers.

Added, 8 Sept. 25

BorderPlex is not an investor or developer. It is a non-profit economic development agency – see https://www.borderplexalliance.org/

The actual infrastructure company engaged through BorderPlex is Stack Infrastructure – their website is https://stackinfra.com

They also have the website datacenters.com, found as https://www.datacenters.com/providers/stack-infrastructure#:~:text=About%20Stack%20Infrastructure&text=The%20company%20delivers%20a%20comprehensive,Virginia%2C%20Portland%20and%20Silicon%20Valley.

Stack Infrastructure is a private company

It was founded in 2018

It is not traded publicly

It’s investors are noted by amount, but names are not disclosed

It is certainly a group of venture capitalists. I’ve worked with a venture capital group, Band of Angels, a transparent group, unlike Stack

They raise money with calls for investors. They have gone through 6 rounds, I believe. This is what start-ups do. It is a start-up company, even after 7 years

Stack Infrastructure does not have a published market capitalization such as publicly traded companies have. It is estimated at a bit over $10B

That is a small fraction of what Stack purports to invest potentially in Project Jupiter. What are the plans for leveraging their investment, and at whose risk?

On its website at https://www.datacenters.com/providers/stack-infrastructure/data-center-locations it claims 76 data centers. Yesterday I saw them individually categorized as operational, under construction, or planned. Most are in the latter categories

The data centers vary in size. “Data center” is a technical term that covers everything from home units to what are called hyperscale (such as Project Jupiter purports to build)

In brief, it has some appearance of a shell game and a short term.

BorderPlex is the public face to New Mexico citizens, but it’s equivalent to the Mesilla Valley Economic Development Agency (Why did it not go through long-standing MVEDA?).

Stack Infrastructure is the group with the money. They are venture capitalists. They are still in start-up mode, which is unusual. Will they stay or leave pieces?

Stack appears to be a shell company, to me. They supposedly build data centers, an extreme technical undertaking for physical construction, spec-ing the data equipment, buying, installing, certifying, and operating the data equipment, doing the same for the Internet connectivity, and, or course, managing the cash flow, debt, apportionment of value to investors, etc.

Six, ten, twenty, or however many venture capitalists are money people, not builders. Whom do they engage / contract with for the phenomenal build-out? Are these stable arrangements? Where are guarantees for investors and esp. for users of the data centers?

Extreme due diligence is in order for Dona Ana County, our citizens, the managers of public infrastructure, and investors. I’ve seen the opposite, to date. Caveat emptor.

ultimate_evaporation_of_discharged_cooling_water_AE_2

https://science-technology-society.com/wp-content/uploads/2023/09/The-advantage-of-analytical-solutions.pdf

stiff ODEs

Here is an exposition of a very useful method of solution:

Precise Calculation of Complex Radioactive Decay Chains

Here is a start

MORE PICTURES TO BE ADDED

METEOROLOGY

Making your own small clouds with a hard squeeze: A plastic bottle, a bit of water, and a match will lead you to appreciate how some clouds form. If you have a thermocouple thermometer, you can dig a bit further. Here’s the link for the full story.

Cloud in a bottle: This is a simple demonstration of phenomena in forming clouds in nature.

Equipment: minimal, cheap.

You fill a clear, squeezable bottle with saturated vapor – you do that by putting a little water in the bottom of the bottle and shaking and swirling it around for, oh, say, a minute. Next, you light a match and put it in the mouth of the bottle and shake it to extinguish the flame and introduce smoke into the bottle, then quickly capping it. If you feel safer, you might light a longer piece of wood, or a cork punk. Now squeeze the bottle hard and then release it sharply. The interior will fill with mist, which is tiny water droplets that condensed around the tinier smoke particles. You can keep squeezing and then releasing the bottle several times to get the effect.

The principle is that the sudden expansion of the air in the bottle decreases its temperature to the point that it is below the condensation point of the water vapor. To put it technically, the expansion is adiabatic, without exchanging any significant heat with the outside air. There are several discussions of the temperature effect, which also explains the decrease of temperature as air goes to higher elevations in steady (nonturbulent) conditions; my explanation using the physics is on another post in these webpages. Of course, the squeezing is the opposite effect. To make the demo more detailed, you can run a fine-wire thermocouple thermometer into the bottle through a tiny hole in the lid, sealing it thoroughly. You can run the thermocouple end to a thermocouple thermometer as I’ve done in this picture. You’ll see the temperature rise on squeezing the bottle and fall on letting it expand.

PICTURE

Video for frames to grab – filling it with a bit of water, shaking it, lighting a match, putting it out to make smoke, sealing the bottle, squeezing it, releasing it, and doing it again

Picture of a cap with a hole

Picture of Omega TCT with lead and with reading

Picture of TC threaded into hole and sealed

Video of squeezing while viewing the TCT and the bottle contents

 

EquipmentSupplies

Let’s try the “Read more” insert. I’ll create the post in text (HTML) and insert “Read more” within this editing environment, which should avoid formatting errors that can occur if it’s inserted within the visual mode Continue reading “Post test read more”

Converting MathType equations to images:

Kutools converted very few equations to images!

Saving a docx as html had the same problem.

Then I simply copied any MT equation, pasted it in a docx like this one, and pasted it in with the 4^th choice, as image!

The choice icon looks like a mountain scene!

Now check that this conversion to image does work. Put this document onto a webpage with Mammoth .docx conveter

1. (in free space). Then

 

 

This is classic one-over-r-squared law for the falloff of power with distance. With R = radius of the Sun (0.696 million km) and R’ = mean radius of the Earth’s orbit (150 million km),

If we want a planet with an energy flux density that’s the same as for Earth (so that it has about the same temperature), we want the total power of the star spread out at the planet’s orbital distance to be like that for the Earth: